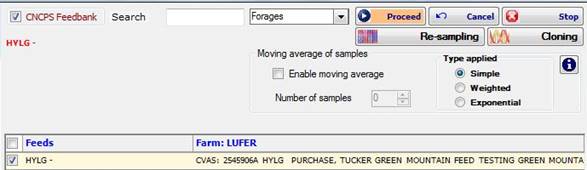
This new feature adds the capability of re-sampling a feed with average values, calculated from a serie of samples, each stored in a different XML file. The term “Moving” indicates that only a sub-set of the available samples is used for the average (typically including the most recent ones); so each time a new sample is added, the last one is excluded from the sub-set. The number of the samples in the sub-set can be chosen for each feed.
Generating Samples
Each time an XML analysis file is imported, its values are also saved as sample data in the NDS database (the first sample is created when the related NDS feed is created and cloned for the first time). The link between the sample and the NDS feed is set through the feed selection step of the resampling.

Moving Average
To apply the moving average, at least two samples for the feed to resample are needed; in this case a panel with some additional controls is displayed:
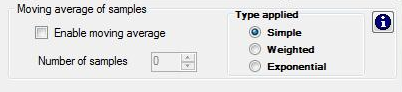
In order to apply the moving average resampling, one has to check the Enable moving average checkbox; the column of the analysis values will change according to the calculus, and a rectangle around the numeric values is displayed to indicate that the values are the result of an average.
Number of samples
If more samples are available you can choose how many of them should be included in the sub-set used to calculate the average values; if this equals or exceeds the number of available samples, the average is calculated using all the available samples. It is also possible to choose just one sample; in this case the resampling is not based on an average, since the values are just those of the most recent sample.
Moving Average variations
Three different average methods are available through a set of radio-buttons:
- Simple (non-weighted) Average
- Linear Weighted Average
- Exponential Average
Simple Moving Average (SMA) is a non-weighted average or, in other words, assigns the same weights to all the sample values.
Since SMA could be disproportionately affected by “old” data, two different weighted average have been developed to give higher weights to the most recent samples and lower weights to the older ones.
Linear Weighted Average assigns decreasing weights as the samples become older, in this way the most recent ones have always the highest weights.
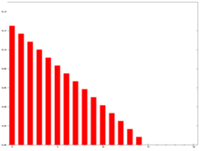
1 Weights in Linear Weighted Average
Exponential Average applies weighting factors which decrease exponentially as the samples become older, with the effect of enhancing even more the recent samples in the average calculation.
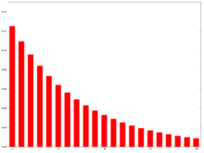
2 Weights in Exponential Average