While Linear Optimization is a deterministic, linear algebra based process, Nonlinear Optimization uses statistical and heuristic based algorithms to optimize the recipes. This means that while Linear Optimization directly calculates the solution, Nonlinear Optimization searches among all the possible recipes given by re-combination of the feeds, according to their constraints, those that minimize or maximize the goal(s) of the optimization.

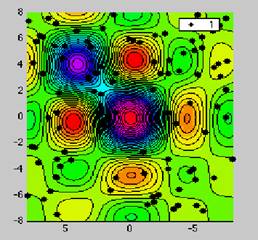
Since a complete search in the Solution Space (including all the optimal and sub-optimal solutions that can be obtained from the original recipe, altering the quantities of its ingredients) could be very time consuming, even for recipes that have a limited number of ingredients, Nonlinear Optimization tries to perform the search only in those solution sub-spaces (sub-sets of the Solution Space) that are more promising in terms of optimality.
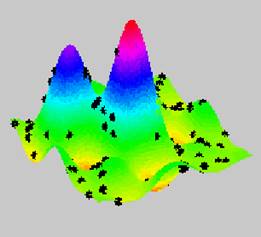
Those sub-spaces are selected by heuristic techniques before being evaluated, with randomness playing a role, since re-combination of the quantities of the feeds partly happens on a random basis; so each optimization session potentially leads to solutions that could differ by small amounts. Feed constraints also play a big role, since their ranges determine the amplitude of the Solution Space. Setting wide ranges between min and max values of feeds or open ranges (without max) increases the amplitude of the Solution Space, thus increasing the number of sub-spaces that have to be evaluated, with the chance in the worst cases of misdirecting the search; beside it could also lead to solutions that are very different from the original recipe. In these cases, one way to re-balance the constraints on the feeds is given by the Create specifications button, that sets the min and max values for each feed using its level in the original recipe as a reference.